[산림경영학] 이자의 종류(단리산, 복리산, 유한연년이자, 유한정기이자, 무한 연년이자 전가식, 무한 정기이자 전가식)

이자의 종류

원금으로 인하여 기말에 가서 얻을 수 있는 이자를 다음기의 원금에 가산하지 않고 원금과 이자액을 매년 일정하게 하는 계산 방식

[공식] N = V(1 + nP) [N:원리합계, V:원금, P:이율, n:기간]

문제) 현재 산림 축적이 1000m³이고, 생장률이 연 3%일 때, 10년 후 산림축적을 단리산법에 의해 구하시오?

1000(1 + 10 x 0.03) = 1,300m³

매기마다 얻은 이자를 다음기의 원금에 가산하여 얻은 원리합계를 다음기의 원금으로 하여 원금과 이자액을 점차 증가시키는 방법

1. 후가식 : 현재 자본금이 V₀이고 이율이 P일 때, n년 후의 자본금 Vₙ 는 [공식] Vₙ = V₀ x 1.0Pⁿ 결론적으로 후가식은 몇 년 후에 얼마가 되느냐?를 계산하는 문제.

문제) 현재 임목축적이 150 m³ 일 때 20년 후 이 산림의 임목축적은? (단, 생장률은 6%)

V = 150 x (1.06)²⁰ = 481.07m³

2. 전가식 : 이율이 P이고 n년 후에 Vₙ의 자본금을 만들려면 현재 자본금 V₀는 [공식] Vₙ = Vₙ / 1.0Pⁿ [ (전가계수) 1 / 1.0Pⁿ ] 결론적으로 전가식은 현재가치가 얼마냐?를 계산하는 문제

문제) 벌기 50년일 때 주벌수입 2,000,000원인 산림의 현재가를 구하시오(연이율 5%)

V = 2,000,000 / 1.05⁵⁰ = 174,407원

1. 후가식 : 매년 말에 r원씩 n회 얻을 수 있는 이자의 후가합계

2. 전가식 : 매년 말에 r원씩 n회 얻을 수 있는 이자의 전가합계

문제) 매년 800,000원씩 조림비를 5년간 지불한다면 마지막 지불이 끝났을 때의 유한연년 수입의 후가합계식을 계산하시오? (단 이율 5%)

1. 후가식 : m년마다 r원씩 n회 얻을 수 있는 이자의 후가합계

2. 전가식 : m년마다 r원씩 n회 얻을 수 있는 이자의 전가 합계

매년 말에 r원씩 영구적으로 얻을 수 있는 전가합계

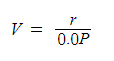
문제) 매년 240만원씩 순수익을 얻을 수 있는 산림을 3,600만원에 구입하였을 때, 연간손익은? (연이율 6%)

V = 2,400,000/0.05 = 40,000,000원

40,000,000 - 3,600,000 = 400만원 이익

4,000,000 x 0.06 = 240,000원 이익

현재부터 m년마다 r원씩 영구적으로 얻을 수 있는 전가합계

문제) 벌기 50년 잣나무림에서 벌기마다 50,000,000원의 수입을 영구히 얻기 위한 전가합계를 구하시오 (단, 연이율 6%, 1.06⁵⁰ = 18.420, 천원이하 반올림) => 정답 2,870,000원